1. 일반
가. 학습 목적
•
컴퓨터 친화적 사고체계에 익숙하여 컴퓨팅 자원을 효율적으로 사용할 수 있는 문제해결역량을 키우기 위해 알고리즘을 학습해야 합니다.
•
자료구조는 알고리즘으로 문제를 해결하기 위해 데이터를 조직화하는 방법이므로 학습해야 합니다.
•
현대 프로그래밍 언어에서 정렬 알고리즘을 제공함에도 여타 다른 정렬 알고리즘을 학습해야 하는 이유는 최적화를 위한 안목을 키우기 위해서 입니다. 라이브러리로 주어진 정렬 알고리즘이 현재 상황에 가장 적절한지 판단하고 더 나은 방법을 찾을 수 있습니다.
나. 자료구조 요약
작업 중
다. 알고리즘 요약
작업 중
2. 자료구조
가. Bag
1) 개념
•
정의: 내부 요소를 삭제할 수 없는 컬렉션 타입입니다.
•
특징: 요소를 수집하고, 내부 요소를 순회하는 기능을 제공합니다.
•
사용 목적: 내부 요소에 대해 삭제와 같은 중간 조작을 허용하지 않고, 요소를 단순 추가하여 데이터의 불변성을 보장해야 하기 위해 사용합니다.
•
사용 예시: 주요 시스템의 로그 보관에 사용할 수 있습니다. 만약 배열이나 리스트를 사용하여 로그를 보관할 경우, 내부 로그 데이터에 대한 조작을 허용하게 됩니다. Bag을 사용하면 앞과 같은 부작용을 제거할 수 있습니다.
2) Bag 내부 구현
•
Bag Data Type API
함수 시그니처 | 설명 |
size(): int | 컬렉션 내부 요소의 전체 개수를 반환합니다 |
add(any): void | 매개변수를 컬렉션 내부 요소로 추가합니다 |
isEmpty(): boolean | 컬렉션 내부 요소의 유무를 반환합니다. 내부 요소가 없다면 true를 반환합니다. |
•
Javascript 구현
class Bag {
#items = [];
isEmpty() {
return this.#items.length === 0;
}
add(item) {
this.#items.push(item);
}
size() {
return this.#items.length;
}
sum() {
return this.#items.reduce((acc, cur) => acc + cur, 0);
}
[Symbol.iterator]() {
let index = 0;
const data = this.#items;
return {
next() {
return index < data.length
? { done: false, value: data[index++] }
: { done: true };
},
};
}
}
JavaScript
복사
나. Stack
1) 개념
•
정의: 마지막으로 삽입된 요소가 가장 먼저 제거(LIFO, last-in first-out, 후입선출)되는 컬렉션 타입입니다.
•
특징: 조회(또는 제거), 삽입의 대상이 되는 요소는 컬렉션 내 마지막 요소입니다. 또한 스택 내 요소를 순차적으로 제거하면, 결과적으로 모든 요소를 역순으로 순회할 수 있습니다.
•
사용 목적: 역방향 순회를 강제해야 하는 경우에 사용됩니다. 가장 마지막에 삽입된(또는 가장 최신) 데이터부터 처리하기 위해 사용합니다.
•
사용 예시: 콜스택과 같이 임시적으로 사용되는 데이터를 다룰 때 자주 사용됩니다.
2) 자바 활용
참고
3) 파이썬 활용
참고
라. Queue & Priority Queue
1) Queue 개념
•
정의: 처음으로 삽입된 요소가 가장 처음 제거(FIFO, first-in first-out, 선입선출)되는 컬렉션 타입입니다.
•
특징: 조회(또는 제거) 대상 요소는 컬렉션 내 마지막 요소이지만, 삽입 시 컬렉션 내 첫번째 요소가 됩니다. 큐 내 모든 요소를 순차적으로 제거하면, 모든 요소를 정방향으로 순회할 수 있습니다.
•
사용 목적: 정방향 순회를 강제 해야 하는 경우에 사용됩니다. 다시 말해, 컬렉션에 삽입한 순서대로 요소를 처리하기 위해 사용합니다.
•
사용 예시: 메시지 큐와 같이 들어온 순서대로 처리해야 하는 데이터를 다룰 때 사용됩니다.
2) Priority Queue 자바 활용
참고
3) 파이썬 활용
참고
마. Linked List
1) 개념
•
정의: 노드 내 데이터와 다른 노드에 대한 참조를 가지고 있는 컬렉션 타입입니다.
•
특징: 노드의 참조를 변경함으로써 요소 변경에 대한 비용이 적습니다.
•
사용 목적: 전체 컬렉션에서 갱신이 빈번하게 일어나는 경우에 사용합니다.
•
사용 예시: 이메일 리스트 관리와 같이 중간의 이메일을 빈번하게 삭제하는 경우에 사용됩니다.
2) Linked List 종류
•
Linked List: 하나의 Node 안에 정보와 레퍼런스(다음 노드의 위치)를 포함하여 노드 간 연결되어 있는 자료구조
•
Singly Linked List: 각 Node는 정보와 하나의 레퍼런스로 구성됨. 하나의 레퍼런스는 뒤의 Node의 위치정보를 포함함
•
Doubly Linked List: 각 Node는 정보와 두 개의 레퍼런스로 구성됨. 각각의 레퍼런스는 앞의 노드와 뒤의 노드의 위치정보를 포함함
•
Circular Linked List: Sinlgy Linked List와 구조적으로 유사하나 마지막 Node의 레퍼런스에 첫번째 Node의 위치정보가 포함됨
3) 성능비교 - Array vs Linked List
•
검색: Array(O(1)), Linked List(O(n))
: Array의 경우 index값을 기준으로 특정 노드의 정보에 직접 접근 가능
: Linked List의 경우, 첫번째 노드부터 순차적으로 확인해야 함
•
앞 삽입 or 삭제: Array(O(n)), Linked List(O(1))
: Array의 경우, Array 중간에 특정 Node를 삽입하거나 삭제 후 뒤의 모든 Node의 인덱스를 수정해야함
: Linked List의 경우, List 중간에 Node를 삽입 또는 삭제 후, 앞뒤 Node의 레퍼런스만 수정하면 됨
•
끝 삽입 or 삭제: Array(O(1)), Linked List(O(n))
: Linked List의 경우 마지막 요소를 탐색해서 삽입 또는 삭제해야 하므로 O(n)이 됨
4) Singly Linked List 구현
참고
5) 자바 활용
참고
6) 파이썬 활용
참고
7) 코틀린 활용
참고
바. Hash
1) 개념
•
정의:
•
특징:
•
사용 목적:
•
사용 예시:
2) 자바 활용
참고
3) 파이썬 활용
참고
사. Graph
1) 개념
•
정의:
•
특징:
•
사용 목적:
•
사용 예시:
2) Graph 세부 특징
•
선형구조로 표현할 수 없는 데이터를 정점과 간선의 구조로 표현하는 자료구조입니다.
•
비선형 자료구조로 정점(노드)와 간선(엣지)로 구성되어 있습니다.
•
노드와 정점은 같은 의미입니다.
•
엣지는 정점 간 연관관계로 정점을 잇는 선으로 표현합니다.
•
엣지는 간선과 같은 의미입니다.
•
인접하다는 것은 정점이 간선으로 연결되어 있다는 뜻입니다.
•
간선은 방향성을 갖는 경우와 가중치는 갖는 경우로 구분 가능합니다.
•
차수란 정점에 속해있는 간선의 개수입니다.
•
경로란 간선으로 연결되어 있는 정점의 집합입니다.
•
순환이란 출발 정점에서 도착 정점으로 돌아올 수 있는 경로입니다.
•
연결 그래프란 모든 정점이 서로 연결된 그래프입니다.
•
비순환 그래프란 순환 경로가 없는 그래프입니다.
•
사용 사례:
◦
소셜 네트워크: 사용자 간의 친구 관계나 팔로우 관계를 표현합니다.
◦
지도: 장소와 그 사이의 경로를 표현합니다.
◦
웹 크롤러: 웹 페이지와 그 사이의 링크를 탐색합니다.
◦
전력 그리드: 발전소, 변전소, 그리고 그 사이의 연결을 표현합니다.
아. Tree
1) 개념
•
정의:
•
특징:
•
사용 목적:
•
사용 예시:
2) 그래프와 트리 관계
image from 곰튀김, 프로그래머스, https://programmers.co.kr/learn/courses/13577#introduction
3) Tree 세부 특징
•
비선형 자료구조의 하나로 데이터 간 연관관계에 방향성과 비순환 특징이 존재합니다.
: 모든 정점이 서로 연결되어 있지만, 순환 경로가 존재하지 않는 그래프입니다. 다시 말해 연결된 비순환 그래프입니다.
: 시작 정점(Root 노드)이 존재하고 두 정점 사이에는 반드시 하나의 방향성이 있는 간선이 존재합니다. 따라서 간선의 수는 전체 정점에서 1을 뺀 만큼 존재합니다.
•
부모와 자식 데이터 간 연관관계를 토대로 저장된 데이터를 빠르게 탐색할 때 사용함. 트리 구조에서 데이터 간 연관관계는 상하위의 레벨에 존재하는 부모 자식 관계만 존재한다. 같은 레벨의 데이터는 연관관계를 갖지 않는다.
→ 이진트리의 경우, 데이터 조회 시 시간복잡도는 O(logn)
→ 부모 노드와 자식 노드로 구성되어 부모 노드의 참조값을 토대로 자식 노드를 탐색할 수 있음
→ 데이터 삽입 규칙: 데이터 탐색이 가능하도록 반드시 부모 노드 이하에 삽입되어야 함. 부모 노드는 반드시 하나만 존재해야 함
→ 데이터 삭제 규칙: 자식 노드가 존재하는 부모 노드가 삭제될 경우, 자식 노드 중 하나가 부모 노드를 대체하도록 재구성해야 한다.
→ 데이터 순회 방법: BFS(레벨 순으로 순회), DFS(root → leaf 방향 순회 반복)
•
사용 사례:
◦
파일 시스템: 디렉토리와 파일의 계층적 구조를 표현합니다.
◦
DOM (Document Object Model): 웹 페이지의 요소와 그 관계를 표현합니다.
◦
이진 탐색 트리: 효율적인 검색, 삽입, 삭제 연산을 위해 사용됩니다.
◦
힙: 우선순위 큐의 구현에 사용됩니다.
4) Binary Search Tree
•
Binary Tree 구조를 유지하면서 이하의 규칙이 추가된 것
•
규칙: 왼쪽 자식 노드는 부모 노드 보다 작을 것, 오른쪽 자식 노드는 부모 노드 보다 클 것
•
노드 삭제 규칙: 삭제된 노드의 왼쪽 자식 노드의 맨 오른쪽 노드의 자식이 삭제된 노드를 대신할 것
•
자바를 활용할 경우, Array에 정의되어 있는 binarySearch를 활용할 수 있다. 이하의 두 코드는 이진 탐색 트리를 사용한 것과 내장 함수를 사용하는 예시이다.
직접 정의 예시
내장 함수 활용 예시
•
이진 검색 활용
class Solution {
public int[] twoSum(int[] numbers, int target) {
int left = 0;
int right = numbers.length - 1;
while (left < right) {
int sum = numbers[left] + numbers[right];
if (sum == target) {
return new int[] {left + 1, right + 1};
} else if (sum < target) {
left++;
} else {
right--;
}
}
throw new IllegalArgumentException("No two sum solution");
}
}
Java
복사
자. Heap
1) 개념
•
정의:
•
특징:
•
사용 목적:
•
사용 예시:
2) Min Heap
•
Binary Tree 구조를 유지하면서 이하의 규칙이 추가된 것
•
규칙: 부모 노드는 항상 자식 노드 보다 작아야 한다
→ 루트 노드가 가장 작은 값을 가진 노드여야 한다
3) 파이썬 활용
참고
3. 알고리즘
가. Sort
1) 정렬 알고리즘 학습 이유
•
대부분의 프로그래밍 언어에서 nlogn 시간복잡도를 갖는 sort API 제공하는데 왜 정렬 알고리즘을 학습해야 하는가?
•
여러 가지 문제해결법 학습: 정렬이라는 목표 달성을 위한 여러 가지 문제해결법이 존재함
•
상황에 따른 문제해결법 학습: 대부분의 요소가 정렬된 경우에는 quick or merge sort 보다 bubble sort가 성능면에서 우월
ex) 사이즈가 작은 컬렉션을 대상으로 대부분의 요소가 정렬된 상태에서 일부의 요소만 정렬이 필요할 경우 Bubble or Insertion Sorting이 성능면에서 우월할 수 있음
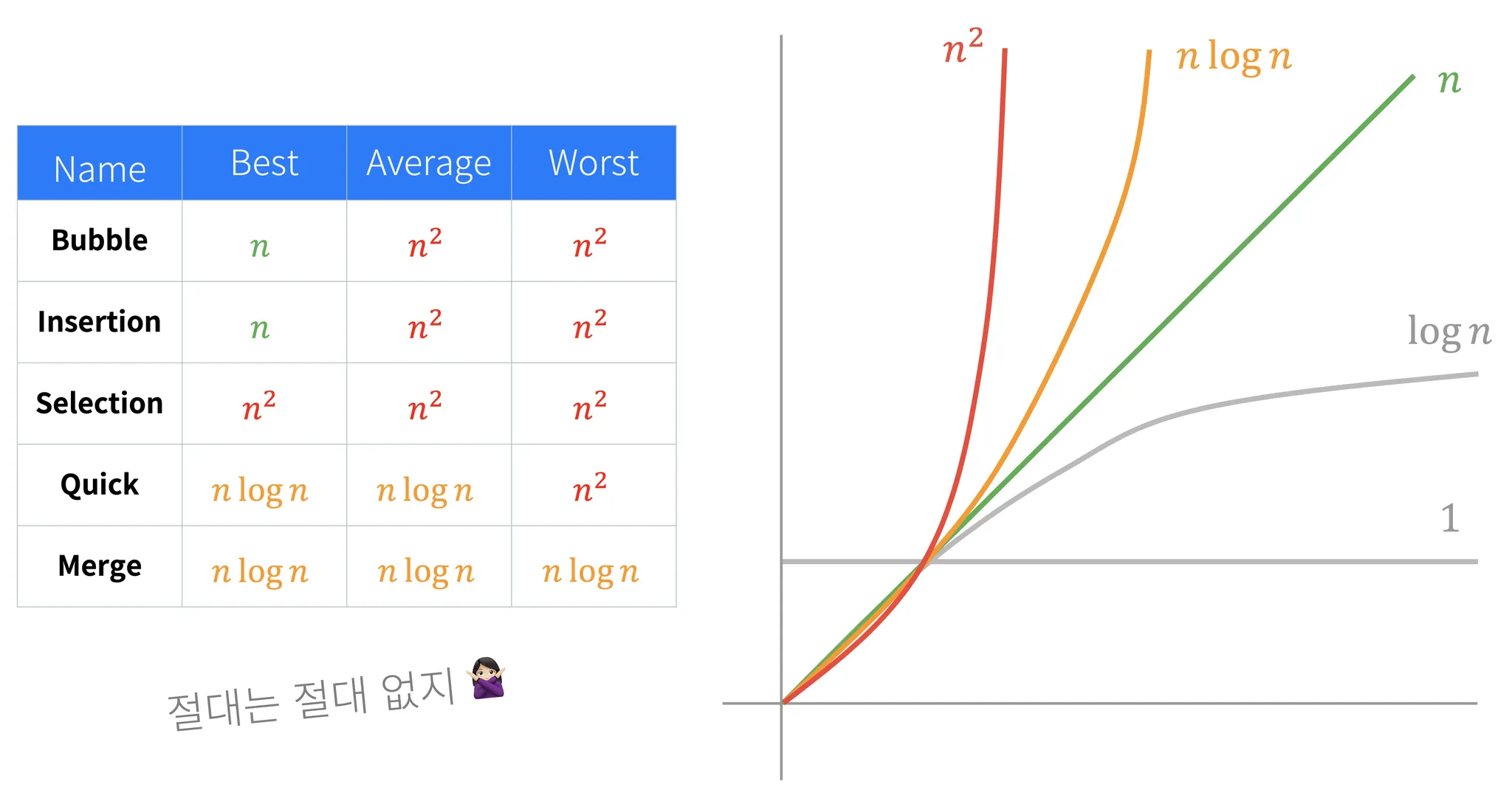
2) 시간복잡도
image from 곰튀김, 프로그래머스, https://programmers.co.kr/learn/courses/13577#introduction
3) Bubble Sort
•
오름차순 정렬을 전제할 경우 왼쪽요소부터 비교해서 크기가 작은 요소가 있다면 오른쪽 요소와 치환하는 것을 반복
•
첫번째 요소를 제외한 나머지 요소를 모두 비교하며 두 번째로 작은 요소를 두번째 위치로 이동
예시
1 3 5 2 4 → 1 3 5 2 4
: 1과 나머지 3, 5, 2, 4를 비교하면 1이 가장 작으므로 첫번째 위치 그대로 유지
1 3 5 2 4 → 1 2 5 3 4
: 3과 나머지 2, 5, 4를 비교하면 2가 가장 작으므로 두번째 위치로 이동하고, 3은 2가 위치했던 곳으로 이동
1 2 5 3 4 → 1 2 3 5 4
: . . .
4) Insertion sort
•
오름차순 정렬을 전제할 경우 왼쪽부터 인접 요소를 비교해서 작은 요소를 왼쪽으로 치환한느 것을 반복
•
만약 이동이 발생하면 이동한 요소를 기준으로 다시 인접 요소 비교
예시
1 3 5 2 4 → 1 3 5 2 4
1 3 5 2 4 → 1 3 5 2 4
1 3 5 2 4 → 1 3 2 5 4
: 5와 2를 비교한 결과 2가 더 작으므로 서로 위치 이동
1 3 2 5 4 → 1 2 3 5 4
: 위치 이동이 발생했으므로 상위 요소 위치 확인 후 3과 2의 위치도 서로 이동
5) Quick Sort
•
Pivot을 설정하고 이를 기준으로 작은 값들의 그룹과 큰 값들의 그룹으로 나눔
•
그룹을 기준으로 다시 pivot을 설정하는 방향으로 더이상 그룹이 생성될 수 없는 상태까지 위의 작업 반복
•
상위 pivot을 기준으로 재결합 과정 반복
6) Merge Sort
•
더 이상 나눠질 수 없을 때까지 전체 길이의 반씩 나누기를 반복
•
나눠진 요소를 다시 합칠(merge) 때 작은 요소를 왼쪽, 큰 요소를 오른쪽으로 위치함
7) Quick Sort vs Merge Sort
•
Quick Sort는 그룹으로 나누는 과정에서 pivot을 기준으로 요소가 정렬됨
•
Merge Sort는 더 이상 나눠질 수 없을 만큼 쪼개진 이후, 결합되는 과정에서 정렬됨
•
둘 다 ‘dive and conquer’ 전략을 채택하지만 정렬되는 순서과 나누는 과정이냐 결합되는 과정이냐에 따라 달라짐
참고) Java Sort
•
Arrays.sort API: primitives 대상 Dual-Pivot Quicksort 알고리즘 활용합니다. 참고로 dual pivot quick sort 알고리즘이란 quick sorting과 유사하나 pivot이 1개가 아닌 2개를 사용하는 차이가 있습니다.
•
Arrays.parallelSort API: multi threading 방식으로 Arrays.sort API 활용합니다.
•
Collections.Sort API: merge sort 알고리즘을 활용합니다.
•
자바의 정렬 알고리즘은 원시 데이터를 직접 변경하므로 부수작용을 고려하여 원본 값을 복사할 필요가 있습니다.
public class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
Set<Integer> result = new HashSet<>();
// Manually creating a sorted copy of the arrays
int[] sortedNums1 = Arrays.copyOf(nums1, nums1.length);
Arrays.sort(sortedNums1);
int[] sortedNums2 = Arrays.copyOf(nums2, nums2.length);
Arrays.sort(sortedNums2);
// Convert the set to an array
return result.stream().mapToInt(x -> x).toArray();
}
}
Java
복사
나. 선형 탐색
다. DFS 그래프 탐색
1) 그래프 탐색
•
그래프 탐색이란 조건에 따라 그래프의 노드를 방문하는 방식의 탐색 알고리즘입니다.
2) 그래프 탐색 동작 원리
•
그래프 탐색은 인접 행렬과 인접 리스트의 방법으로 구현할 수 있습니다. 인접 행렬의 경우, 정점의 수(V)의 제곱 만큼의 메모리를 사용하기 때문에 비효율적입니다.
•
인접 리스트의 경우 시공간 효율성이 대부분의 경우 만족되기 때문에 인접 리스트 방식을 사용합니다.
•
인접 리스트 방식의 공간 복잡도는 정점의 수와 간선의 수의 합에 해당합니다. 시간 복잡도의 경우 ~~
3) 재귀 활용 DFS, 스택 활용 DFS, 큐 활용 BFS
재귀 활용 DFS
스택 활용 DFS
큐 활용 BFS
4) DFS와 백트래킹
백트래킹 설명
연관 코드
5) DFS와 순열조합
•
순열 접근
class Solution {
List<List<Integer>> answer = new ArrayList<>();
boolean[] visited ;
public List<List<Integer>> permute(int[] nums) {
visited = new boolean[nums.length];
dfs(nums, new ArrayList<>());
return answer;
}
void dfs(int[] nums, List<Integer> left) {
if (left.size() == nums.length) {
answer.add(new ArrayList<>(left));
return;
}
for (int i = 0; i < nums.length; i++) {
if (visited[i]) continue;
visited[i] = true;
left.add(nums[i]);
dfs(nums, left);
left.remove(left.size() - 1);
visited[i] = false;
}
}
}
Java
복사
•
조합 접근
class Solution {
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
dfs(n, k, new ArrayList<>(), 1);
return result;
}
void dfs(int n, int k, List<Integer> cur, int start) {
if(cur.size() == k){
result.add(new ArrayList<>(cur));
return;
}
for(int i = start; i <= n; i++){
cur.add(i);
dfs(n, k, cur, i + 1);
cur.remove(cur.size() - 1);
}
}
}
Java
복사
4) DFS 재귀 vs 스택 구현
•
DFS는 재귀와 스택의 형태로 구현할 수 있습니다. 재귀의 경우 보다 우아하게 풀어낼 수 있다는 점에서 코테에서 많이 활용됩니다. 참고로 백트랙킹의 원리를 활용해서 탐색의 효율성을 높일 수 있습니다. 예를 들어, 탐색 중간에 그만둘 수 있는 조건을 활용하여 재귀함수를 얼리 리턴하는 방식으로 탐색할 수 있습니다.
재귀 활용 DSF 구현 코드
스택 활용 DFS 구현 코드
•
그래프 모양이 아니더라도 문제를 해석하기에 따라 그래프로 변환할 수 있습니다. 예를 들어, 이하의 육지찾기 문제의 경우에도 육지를 문자 ‘1’, 바다를 ‘0’으로 잡고 찾은 육지를 바다로 변경하는 방식으로 DFS로 쉽게 풀어낼 수 있습니다.
•
재귀 활용 시, 재귀 종료와 가지치기 그리고 결과 값을 저장하는 로직에 대한 설계가 중요합니다. 이하의 코드에서 재귀 종료와 가지치기, 결과값 저장 코드를 비교해볼 필요가 있습니다.
예시 코드
5) DFS 그래프 노드 간 연결성 확인
•
DFS를 활용하여 특정 노드의 연결여부를 확인할 수 있습니다. 우선 특정 노드를 선택하여 연결되어 있는 모든 노드를 확인합니다. 더이상 연결할 수 없다면, 연결성 확인 인덱스를 높인 후, 연결되어 있지 않은 다른 노드를 선택하여 앞의 과정을 반복합니다. 모든 노드를 대상으로 탐색했다면, 연결성을 확인할 노드와 연결성 확인 인덱스를 비교하며 연결성을 확인할 수 있습니다.
6) DFS 활용 그래프 순환구조 판별
라. BFS 그래프 탐색
1) BFS 동작 원리
2) BFS 활용법
•
그래프의 최단 경로 탐색과 같이 다익스트라 알고리즘을 구현할 때 활용합니다. DFS와 달리 재귀를 활용한 풀이가 어렵습니다. 이와 같은 이유로 재귀 활용이 가능한 DFS 방식으로 그래프 탐색 문제에 접근하는 것이 시간 절약 측면에서 낫습니다.
3) 경우의 수와 조합
•
DFS는 조합 문제에 대한 접근 방법으로도 출제됩니다. 특정 조건에 따라 조합 가능한 경우의 수를 그래프 형태로 해석하여 모든 노드를 탐색하는 방향으로 문제를 해결할 수 있습니다. 조합의 경우, 중간 노드의 값은 최종 결과를 얻기 위한 값으로 활용하고 마지막 리프 노드에서 얻어지는 값을 활용하여 문제를 해결할 수 있습니다. 이하의 코드는 마지막 노드값만 의미가 있습니다.
예시 코드
리트코드 연관 문제
4) BFS로 트리 순회
연습 문제 참고
마. 재귀와 동적 프로그래밍
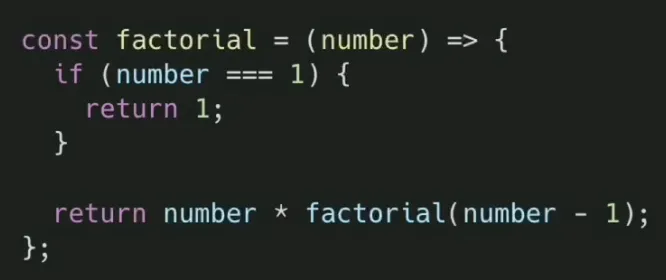
1) 재귀란
•
재귀 함수는 Base Case와 Recursive Case로 구성되어 있습니다. 전자는 무한 호출을 방지하기 위해 함수가 끝나는 조건이 명시되어 있습니다. 후자는 함수의 본문으로 문제를 작게 쪼개기 위해 자기 자신을 호출합니다.
2) 재귀함수가 유용한 두 가지 경우
•
문제를 여러 단계에 걸쳐서 파고들 때 유용합니다.
•
상위의 문제를 하위 문제로 쪼개고, 하위 문제의 결과를 기반으로 상위 문제를 해결할 수 있을 때 유용합니다.
3) 재귀함수 작성 방법
•
우선적으로 Base Case 정의하기 위해 더 이상 자기 자신을 호출할 필요가 없는 경우를 찾아야 합니다.
•
Base Case의 직전 단계를 생각해야 합니다. 아래와 같은 절차에 따라 Base Case의 직전 단계를 상상해보고 그에 따라 Recursive Case를 정의할 수 있습니다.
4) 재귀함수 단점
•
함수는 부모 함수에서 자식 함수를 호출한다고 가정할 때 콜스택에서 부모 함수와 자식 함수를 모두 관리합니다. 재귀함수의 경우, 콜스택에 자기 자신을 계속 쌓게됩니다.
•
꼬리재귀함수의 경우, 콜스택을 거치지 않고도 돌아갈 곳을 알기 때문에 메모리를 아낄 수 있습니다
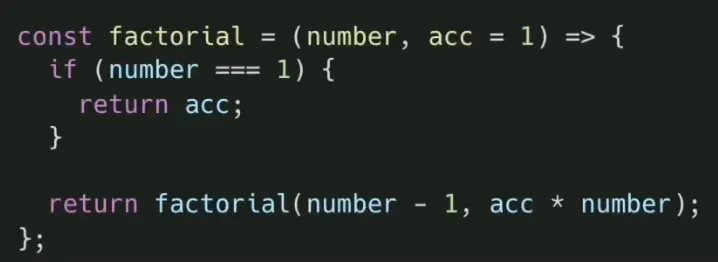
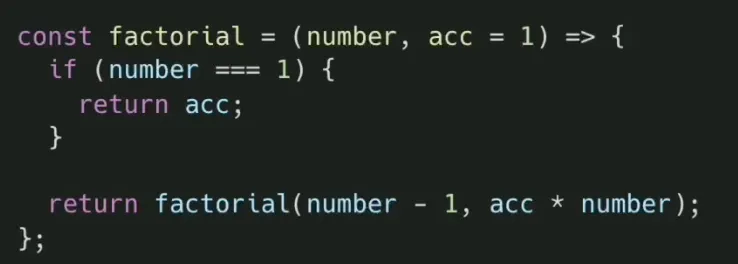
5) 재귀 → 꼬리재귀로 최적화
•
함수 본문의 계산 로직과 로컬 변수를 함수의 매개변수로 전달함으로써 스택에 사용될 여지를 제거해야 합니다.
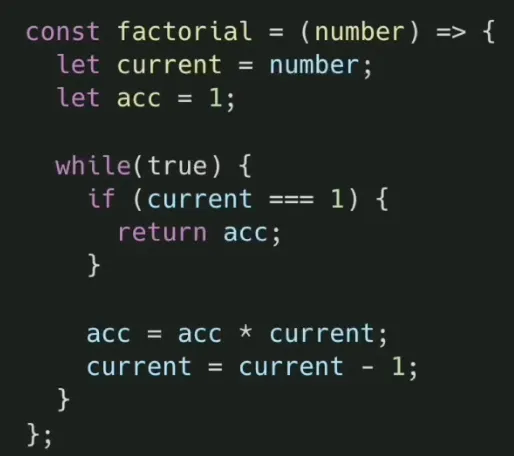
6) 꼬리재귀 → 반복문 변경
6) 동적계획을 이용한 최적화
동적 계획법의 핵심은 작은 문제의 결과를 재사용하여 큰문제를 보다 효율적으로 해결하는 것이다.
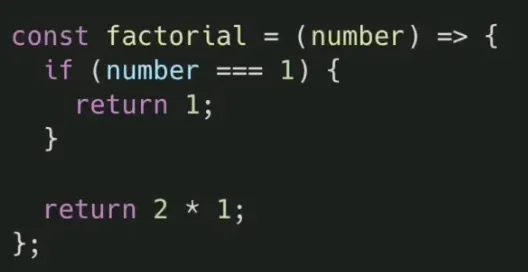
•
재귀방식으로 피보나치 수열을 구현하면 시간 복잡도는 O(N^2)임
const fibonacci = (n) => {
if (n === 0) {
return 0;
}
if (n === 1) {
return 1;
}
return fibonacci(n - 2) + fibonacci(n - 1);
}
JavaScript
복사
•
이미 계산된 함수를 재귀의 형태로 다시 반복 사용하는 경우가 많기 때문에 시간복잡도가 크다
예시
•
하향식 동적계획(메모이제이션)을 활용하면 이미 계산한 값을 캐시에 저장해두고 필요할 때마다 가져다 쓰는 방법입니다. 큰 문제를 작은 문제로 나눈다는 점에서 재귀와 방향은 비슷합니다.
const fibonacci = (n, memo = []) => {
if (n === 0) {
return 0;
}
if (n === 1) {
return 1;
}
if (!memo[n]) {
memo[n] = fibonacci(n - 2, memo) + fibonacci(n - 1, memo)
}
return memo[n];
}
JavaScript
복사
•
상향식 동적계획은 작은 문제를 해결하여 큰 문제를 해결하는 것이 핵심입니다. 재귀 대신에 반복문 등의 다른 방법으로 접근해야 합니다.
•
이하의 코드의 경우, counter == n이 될때까지 꼬리 재귀를 반복하며 이전의 값을 매개변수로 전달하고 있습니다.
const fibonacci = (n, counter = 2, prev = 0, curr = 1) => {
if (n === 0) {
return 0;
}
if (n === 1) {
return 1;
}
if (n === counter) {
return prev + curr;
}
return fibonacci(n, counter + 1, curr, prev + curr);
}
JavaScript
복사
바. 그리디 알고리즘
1) 그리디 알고리즘 vs 동적 계획법 vs 분할 정복
•
최적 부분 구조: 부분에 대한 해결을 쌓아서 전체 문제를 해결할 수 있는 것
•
탐욕 선택 속성: 항상 그 시점에 최적의 것을 선택할 수 있는 것
•
중복된 하위 문제들: 탐욕 선택 속성과 다르게 항상 특정 시점에 최적의 것을 선택하는 거이 아니라, 부분에 대한 해결을 찾고 합해서 전체 문제를 해결하는 것
image from 박상길, 자바 코틀린 알고리즘 인터뷰
4. 문자열 다루기
가. 문자 타입 변환
1) 문자열  문자 배열
문자 배열
char[] chars = s.toCharArray();
String newString = String.valueOf(chars);
Java
복사
나. 문자열 다루기 패턴
1) 문자열 내 중복 제거 - Set 활용
String str = "programming";
Set<Character> charSet = new HashSet<>();
for (char c : str.toCharArray()) {
charSet.add(c);
}
// Set을 String으로 변환
String result = charSet.stream()
.map(String::valueOf)
.collect(Collectors.joining());
Java
복사
2) 중복 문자 카운팅 - HashMap 활용
String str = "programming";
Map<Character, Integer> charCountMap = new HashMap<>();
for (char c : str.toCharArray()) {
charCountMap.put(c, charCountMap.getOrDefault(c, 0) + 1);
}
for (Map.Entry<Character, Integer> entry : charCountMap.entrySet()) {
System.out.println(entry.getKey() + ": " + entry.getValue());
}
Java
복사
3) 스페이스를 포함한 공백 제거 - 정규표현식
다. 문자열 정렬
1) 문자열 내 문자 정렬
String original = "banana";
char[] chars = original.toCharArray();
Arrays.sort(chars);
String sorted = new String(chars);
Java
복사
2) 문자 커스텀 정렬
String original = "HelloWorld";
char[] chars = original.toCharArray();
// 커스텀 Comparator를 사용하여 문자 배열을 역순으로 정렬
Arrays.sort(chars, Comparator.comparingInt(c -> -c));
String sorted = new String(chars);
Java
복사
3) 문자열 역순 정렬: String과 같은 Object 타입에 대해서는 Comparator.reverseOrder() 사용할 수 있다
String[] result = s.split("\\s+");
Arrays.sort(result, Collections.reverseOrder());
Kotlin
복사
3) 문자열 리스트 정렬
List<String> strings = Arrays.asList("banana", "apple", "cherry");
Collections.sort(strings);
List<String> strings = Arrays.asList("banana", "apple", "cherry");
strings.sort(Comparator.naturalOrder());
Java
복사
라. 문자열과 람다
1) IntStream 활용하여 인덱스 순회
public class Solution {
public String mergeAlternately(String word1, String word2) {
StringBuilder result = new StringBuilder();
int maxLength = Math.max(word1.length(), word2.length());
IntStream.range(0, maxLength).forEach(i -> {
if(i < word1.length()) result.append(word1.charAt(i));
if(i < word2.length()) result.append(word2.charAt(i));
});
return result.toString();
}
}
class Solution {
public String mergeAlternately(String word1, String word2) {
StringBuilder result = new StringBuilder();
int maxLength = Math.max(word1.length(), word2.length());
for(int i = 0; i < maxLength; i++){
if(i < word1.length()){
result.append(word1.charAt(i));
}
if(i < word2.length()){
result.append(word2.charAt(i));
}
}
return result.toString();
}
}
Kotlin
복사
마. 문자열 기타
1) StringBuilder 활용
StringBuilder sb = new StringBuilder();
for (char c : charSet) {
sb.append(c);
}
String result = sb.toString();
Java
복사
2) 문자열 내 특정 문자 존재여부 확인
String stones = "afdsfsafdsfds"
String jewels = "ab"
for(char stone : stones.toCharArray()){
if(jewels.indexOf(stone) != -1){
stoneCounter.put(stone, stoneCounter.getOrDefault(stone, 0) + 1);
}
}
Java
복사
Reference
•
Singly Linked List 구현, 엔지니어대한민국, https://www.youtube.com/user/damazzang/videos
•
quick sort vs merge sort, https://www.geeksforgeeks.org/quick-sort-vs-merge-sort/